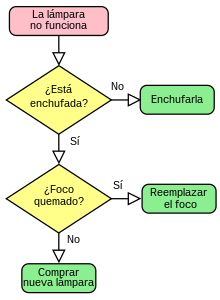
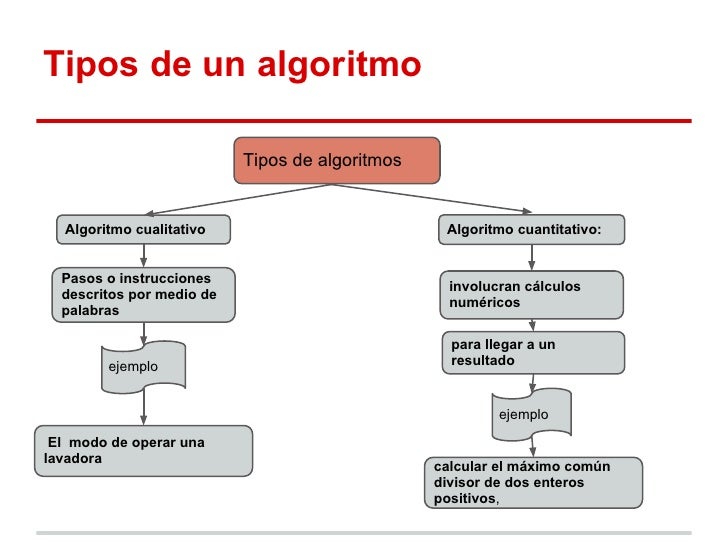
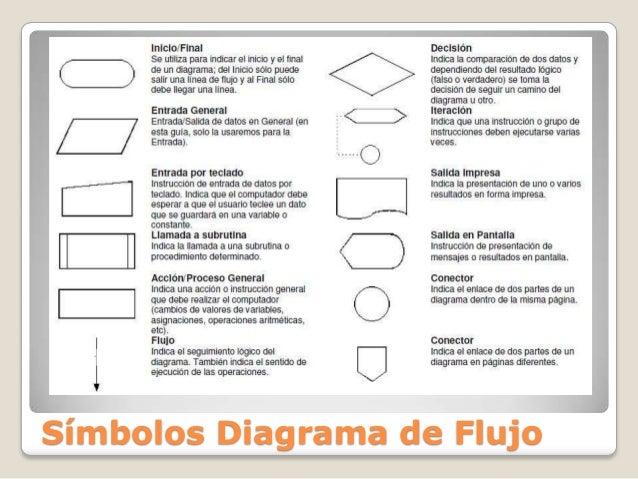
Tipos De Datos
Todos los datos tienen un tipo asociado con ellos. Un dato puede ser un
simple carácter, tal como ‘b’, un valor entero tal como 35. El tipo de dato
determina la naturaleza del conjunto de valores que puede tomar una variable.
Numéricos
Simples Lógicos
Alfanuméricos (string)
Tipos de
datos Arreglos (Vectores, Matrices)
Estructurados Registros
(Def. por el Archivos
usuario) Apuntadores
Tipos de Datos Simples
Datos Numéricos: Permiten representar valores escalares de forma numérica,
esto incluye a los números enteros y los reales. Este tipo de datos permiten
realizar operaciones aritméticas comunes.
Datos Lógicos: Son aquellos que solo
pueden tener dos valores (cierto o falso) ya que representan el resultado de
una comparación entre otros datos (numéricos o alfanuméricos).
Datos Alfanuméricos (Stirling): Es una secuencia de caracteres alfanuméricos
que permiten representar valores identificables de forma descriptiva, esto
incluye nombres de personas, direcciones, etc. Es posible representar números
como alfanuméricos, pero estos pierden su propiedad matemática, es decir no es
posible hacer operaciones con ellos. Este tipo de datos se representan
encerrados entre comillas.
Ejemplo:
“Instituto Tecnológico de Tuxtepec”
“1997”
Operadores y Operando
Operadores: Son elementos que relacionan de forma diferente, los valores de
una o más variables y/o constantes. Es decir, los operadores nos permiten
manipular valores.
Aritméticos
Tipos de Operadores Relaciónales
Lógicos
Operadores Aritméticos: Los
operadores aritméticos permiten la realización de operaciones matemáticas con
los valores (variables y constantes).
Los operadores aritméticos pueden ser utilizados con tipos de datos enteros
o reales. Si ambos son enteros, el resultado es entero; si alguno de ellos es
real, el resultado es real.
Operando (Operador) Operando
Valor
(Constante o variable)
Operadores Aritméticos
+ Suma
- Resta
* Multiplicación
/ División
Mod Modulo (residuo de la división entera)
Ejemplos:
Expresión Resultado
7 / 2 3.5
12 mod 7 5
4 + 2 * 5 14
Prioridad de los Operadores Aritméticos
Todas las expresiones entre paréntesis se evalúan primero. Las expresiones
con paréntesis anidados se evalúan de dentro a fuera, el paréntesis mas interno
se evalúa primero.
Dentro de una misma expresión los operadores se evalúan en el siguiente
orden.
1.- ^ Exponenciación
2.- *, /, mod Multiplicación, división, modulo.
3.- +, - Suma y resta.
Los operadores en una misma
expresión con igual nivel de prioridad se evalúan de izquierda a derecha.
Operadores Relaciónales:
Se utilizan para establecer una relación entre dos valores.
Compara estos valores entre si y esta comparación produce un resultado de
certeza o falsedad (verdadero o falso).
Los operadores relaciónales comparan valores del mismo tipo (numéricos o
cadenas)
Tienen el mismo nivel de prioridad
en su evaluación.
Los operadores relaciónales tiene menor prioridad que los aritméticos.
Operadores Relaciónales
> Mayor que
< Menor que
> = Mayor o igual que
< = Menor o igual que
< > Diferente
= Igual
Ejemplos:
Si a = 10 b = 20 c = 30
a + b > c Falso
a - b < c Verdadero
a - b = c Falso
a * b < > c Verdadero
Ejemplos no lógicos:
a < b < c
10 < 20 < 30
T < 30 (no es lógico porque tiene diferentes operandos)
Operadores Lógicos:
Estos operadores se utilizan para establecer relaciones entre valores
lógicos.
Estos valores pueden ser resultado de una expresión relacional.
Operadores Lógicos
And Y
Or O
Not Negación
Operador And
Operando1 Operador Operando2
Resultado
T AND T T
T F F
F T F
F
F F
Operador Or
Operando1 Operador Operando2
Resultado
T OR T T
T
F T
F
T T
F F F
Operador Not
Operando Resultado
T F
F T
Ejemplos:
(a < b) and (b < c)
(10<20) and (20<30)
T and T
T